WAHLPFLICHTBEREICH MODELLIERUNG MECHANISCHER UND DYNAMISCHER SYSTEME
Modellierung mechanischer Strukturen
Die Modellierung mechanischer Strukturen nimmt eine Schlüsselrolle in der Entwicklung neuer Materialien ein, die in den verschiedensten Bereichen zum Einsatz kommen, z.B.
- Luft- und Raumfahrt, Automobilbau,
- Verfahrenstechnik, Ablaufplanung, Anlagenbau,
- Materialprüfung, Materialwissenschaften,
- Robotik, Biomechanik, Medizintechnik.
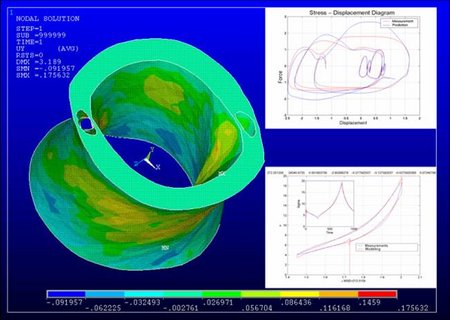
Beispiele sind ein Flugzeugflügel oder der Flügel einer Windkraftanlage, die in Bezug auf Belastbarkeit optimiert werden sollen: Einerseits können hierzu Form und die zum Bau verwendeten Materialien variiert werden, andererseits sind dabei aber Größen wie z.B. das Gewicht zu berücksichtigen. Ziel der Optimierung ist etwa die Rissbildung aufgrund von Materialermüdung zu verringern.
Allgemein besteht die Modellierung einer mechanischen Struktur aus zwei Arbeitsschritten:
- Aufstellung eines mathematischen Modell, welches die Zusammenhänge in dem vorliegenden mechanischen System beschreibt,
- Analyse des erstellten Modells: Herleitung und Berechnung von Lösungen mit Hilfe geeigneter analytischer und numerischer Verfahren.
Mechanische Systeme und Strukturen werden je nach technischer Fragestellung durch Gesetze der
- Mechanik starrer Körper – Massepunkte und nicht deformierbare Körper,
- Kontinuumsmechanik – deformierbare Körper, innere Verschiebungen und Spannungen in Körpern
beschrieben.
Beispiele für Starrkörpersysteme sind Bauteile eines PKW-Bremssystems (Bremsbeläge, Kolben und Bremssattel, die durch Federn und Dämpfer verbunden sind), Roboter, aber auch Apparate mit Anwendungen in Biomechanik oder Medizin (z.B. Prothesen).
Die Kontinuumsmechanik findet in vielen Bereichen Einsatz in der Entwicklung von Produkten und technischen Geräten. Durch die Berücksichtigung von Materialeigenschaften, Verformungen und Spannungen können gezielt Abläufe und Eigenschaften optimiert werden, aber auch Festigkeit und Lebensdauern analysiert werden. Anwendungen liegen im Bereich Materialentwicklungen in der Fahrzeugindustrie (Belastungen bei Unfällen), aber auch in der Entwicklung von Modellen zur Beschreibung der Belastung und Verformung im menschlichen Körper (mit Anwendungen in der Medizin, Biomechanik, plastischen Chirurgie).
In den Modellen werden gewöhnliche und partielle Differentialgleichungen sowie analytische und numerische Verfahren verwendet. Grundlagen der Mechanik sowie Kompetenzen in analytischen und numerischen Verfahren werden im Rahmen der Lehrveranstaltungen vermittelt und ermöglichen, für eine mit einer mechanischen Struktur zusammenhängende Fragestellung ein mathematisches Modell aufzustellen, begründet einen analytischen oder numerischen Lösungsansatz zu wählen, und diesen mit Hilfe von fertigen Softwarepaketen oder selbst entwickelten Programmen umzusetzen und die erzielten Ergebnisse zu analysieren.
Modellierung dynamischer Systeme
Ein dynamisches System ist ein Ausschnitt der Wirklichkeit, dessen zeitlichen Verlauf man studieren will. Beispiele sind:
- Mechanische Systeme: Maschinen, Roboter, Satelliten, Fahrzeuge,
- Elektrodynamische Systeme: Schaltkreise, Computer, Autoelektronik, Quantengatter,
- Biologische Systeme: Zellkulturen, Körperorgane, Tierpopulationen, Ökosysteme,
- Wirtschaftliche Systeme: Produktionsprozesse, logistische Abläufe, Märkte, Volkswirtschaften.
Man ist daran interessiert, wie sich das Verhalten solcher Systeme mit der Zeit ändert. Diese zeitliche Entwicklung wird mathematisch typischerweise durch Differenzen- und Differentialgleichungen beschrieben. Die Theorie dynamischer Systeme interessiert sich aber nicht so sehr für die numerische Berechnung dieser zeitlichen Entwicklung, sondern eher für qualitative Aspekte.
Typische Fragestellungen sind: Treten Gleichgewichtslagen auf? (Marktgleichgewichte, ökologische Gleichgewichte) Sind diese stabil oder instabil? Gibt es periodische Lösungen? (Schwingungen, Populations- oder Konjunkturzyklen) Wird das Systemverhalten chaotisch? Sind Aussagen über die langfristige Entwicklung des Systems möglich?
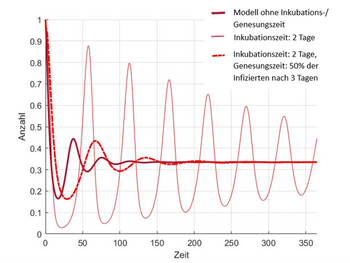
Die Abbildungen zeigen Berechnungen einer Epidemie auf der Basis von Delay-Differenzialgleichungen für die Beschreibung von infizierten und infizierbaren Personen unter Berücksichtigung einer endlichen Inkubationszeit und Genesungszeit. In der Animation variiert die Inkubationszeit von 0 bis 4 Tage. Die Ergebnisse veranschaulichen, wie eine kurze oder längere Inkubations- bzw. Genesungszeit den zeitlichen Verlauf beeinflusst.